Math On Bias and Variance
First we already have a great post.
Trade-offs are everywhere. As an EE undergraduate taking courses in circuits, I was taught how circuit design is a game of trade-offs and there is never free lunch: we have to trade one thing for other desirable properties.
For example, in analog design, we have to consider many aspects of the circuit performance such as linearity, noise, input/output impedance, stability, and voltage swings. Normally we cannot optimize all of these parameters and have to trade some aspects for others. Sometimes we have to resort to trials and errors by treaking the dials and knobs available to us.
Therefore, it isn’t surprising for me to come across tradeoff again in machine learning.
What is a bias-variance tradeoff? It refers to the situations where models have a lower bias in parameter estimation have a higher variance of the parameter estimates across samples, or vice versa. Starting from the definition of variance: \({ \operatorname {Var} [X]=\operatorname {E} [X^{2}]-{\Big (}\operatorname {E} [X]{\Big )}^{2}.}\)
\({ \operatorname {Err} (x)=\operatorname {E} [Y^{2}]-{\Big (}\operatorname {E} [X]{\Big )}^{2}.}\)
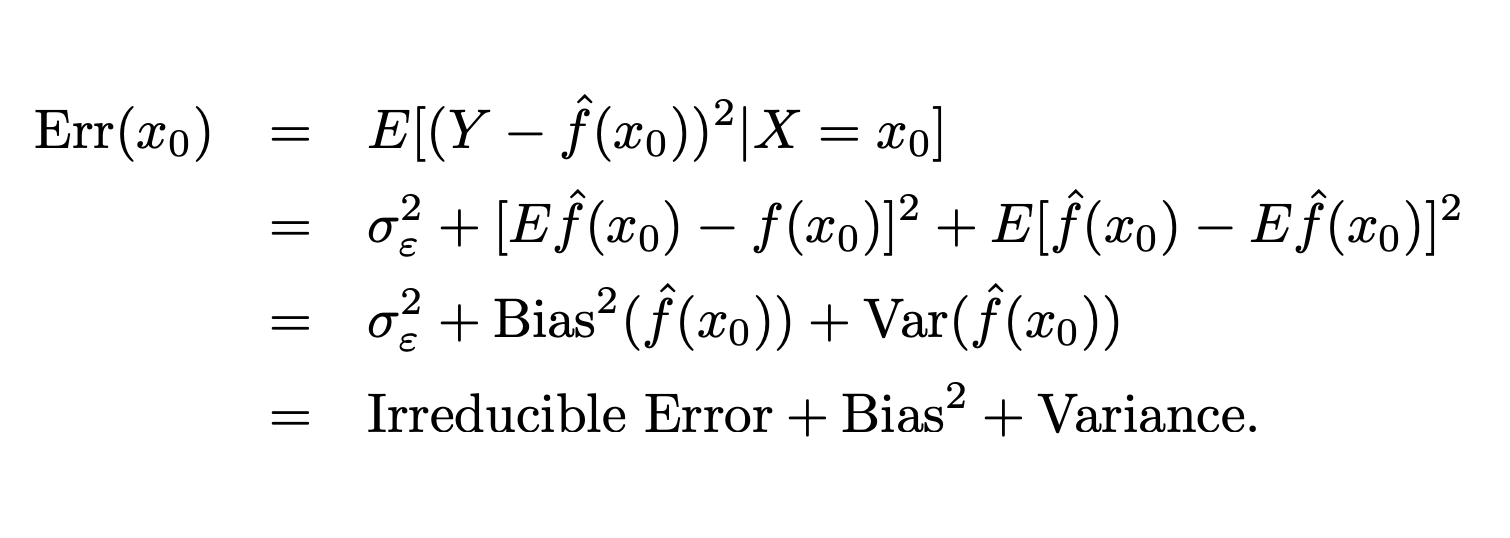
A illustration from Choosing Prediction Over Explanation in Psychology: Lessons From Machine Learning
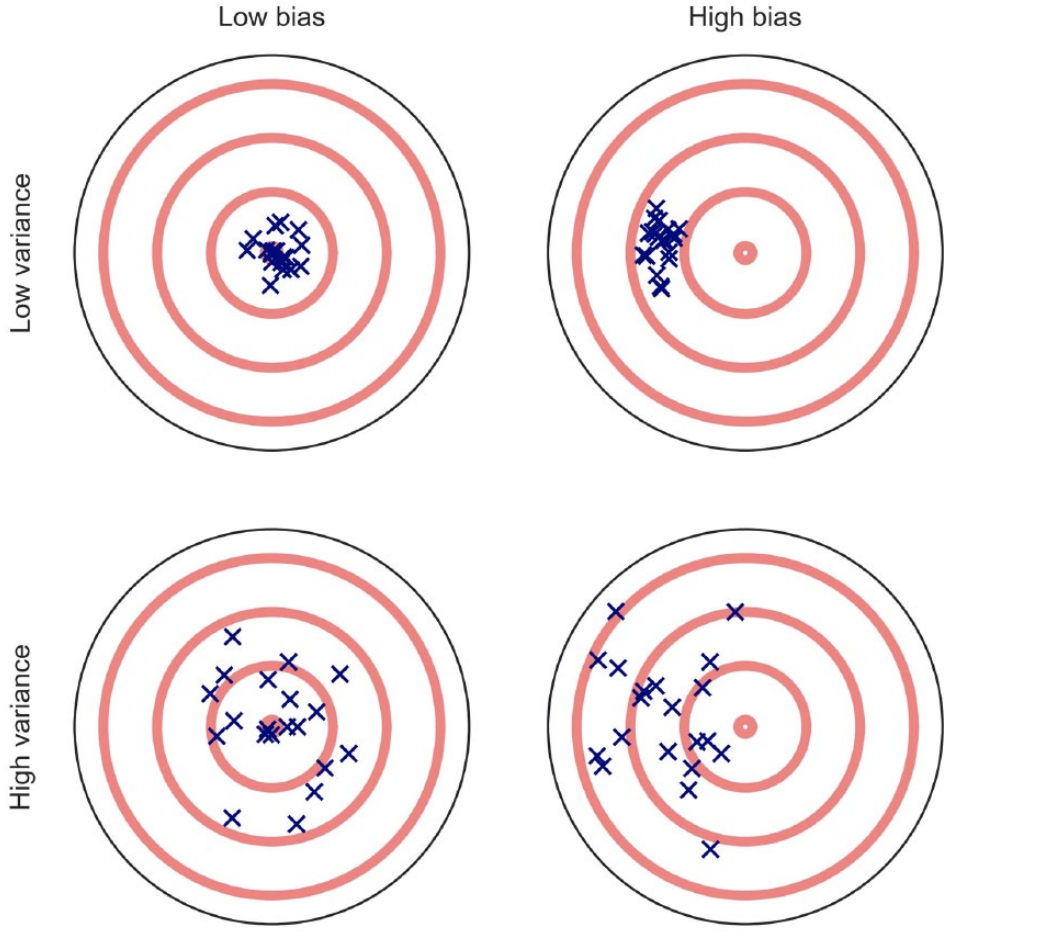An estimator’s predictions can deviate from the desired outcome (or true scores) in two ways.
First, the predictions may display a systematic tendency (or bias) to deviate from the central tendency of
the true scores (compare right panels with left panels). Second, the predictions may show a high degree
of variance, or imprecision (compare bottom panels with top panels).
References:
3.Analog Design Trade-Offs in Applying Linearization Techniques Using Example CMOS Circuits