The course slides:

1.Intro and motivation

Motivation

  • Optimization algorithms are the basic engine behind deep learning methods that enable methods to learn from data by adapting their parameters.

  • They solve the problem of the minimization of an objective function that measures the mistakes made by the model.
    • e.g. prediction error(classification), negative reward(reinforcement learning)
  • Work by making a sequence of small incremental changes to model parameters that are each guaranteed to reduce the objective by some small amount.

Basic notation

  • Parameters \(\theta \in R^n\)

  • Real-valued objective function \(h(\theta)\)

  • Goal of optimization \(\theta^* = argmin h(\theta)\)

Example: neural metwork training objective

  • The standard neural network training objective is given by:

\(h(\theta)=\frac{1}{m} \sum_{i=1}^m \ell(y_i, f(x_i, \theta))\)

2.Gradient descent

Gradient descent: definition

  • Basic gradient descent iteration: \(\theta_{k+1} = \theta_k - \alpha_k \nabla h(\theta_k)\)

Intuition: gradient descent is “steepest descent”

  • Gradient direction $\nabla h(\theta_k)$ gives greatest reduction in $h(\theta_k)$ per unit of change in $\theta$.

  • If $\nabla h(\theta_k)$ is “sufficiently smooth”, and learning rate small, gradient will keep pointing down-hill over the region in which we take our step.

Intuition: gradient descent is minimizing a local approximation

  • 1st-order Taylor series for around current $\theta$ is

  • For small enough d this will be a reasonable approximation

  • Gradient update computed by minimizing this within a sphere of radius r

The problem with gradient descent

High - diverge Low - Converge very slowly

Convergence theory: technical assumptions

  • $h(\theta)$ has Lipchistz continuous derivatives

\(\lVert \nabla h(\theta) - \nabla h(\theta') \rVert \leq L \lVert \theta - \theta' \rVert\)

  • is strongly convex (perhaps only near minimum) \(h(\theta + d) \geq h(\theta) + \nabla h(\theta)^\top d + \frac{\mu}{2} \lVert d \rVert^2\)
  • For now: gradients are computed exactly (i.e. without approximations/not stochastic)

Convergence theory: upper bounds

If previous conditions hold and we take

Number of iterations

Convergence theory: useful in practice?

  • Issues with bounds such as this one:
    • too pessimistic (they must cover worst-case examples)
    • Some assumptions too strong (e.g. convexity)
    • Other assumptions too weak (real problems have additional useful structure)
    • Rely on crude measures of objective (e.g. condition numbers)
    • Usually focused on asymptotic behavior (do care how quickly you are getting to a point preaymptotically)
  • The design/choice of an optimizer should always be informed by practice more than anything else. But theory can help guide the way and build intuitions.

3.Momentum methods

The momentum method

  • Motivation
    • the gradient has a tendency to flip back and forth as we take steps when the learning rate is large
    • e.g. the narrow valley
  • The key idea:
    • accelerate movement along directions that point consistently down-hill across many consecutive iterations (i.e. have low curvature)
  • How?
    • treat current solution for like a ball rolling along a surface whose height is given by, subject to the force of gravity

Defining equations for momentum

Define

  • Learning rate: $\alpha_k$

  • Momentum constant: $\eta_k$

  • Classical Momentum \(v_{k+1} = \eta_k v_k - \nabla h(\theta_k)\)
  • Nesterov’s variant \(v_{k+1} = \eta_k v_k - \nabla h(\theta_k+\alpha_k \eta_k v_k)\)

Narrow 2D valley example revisited

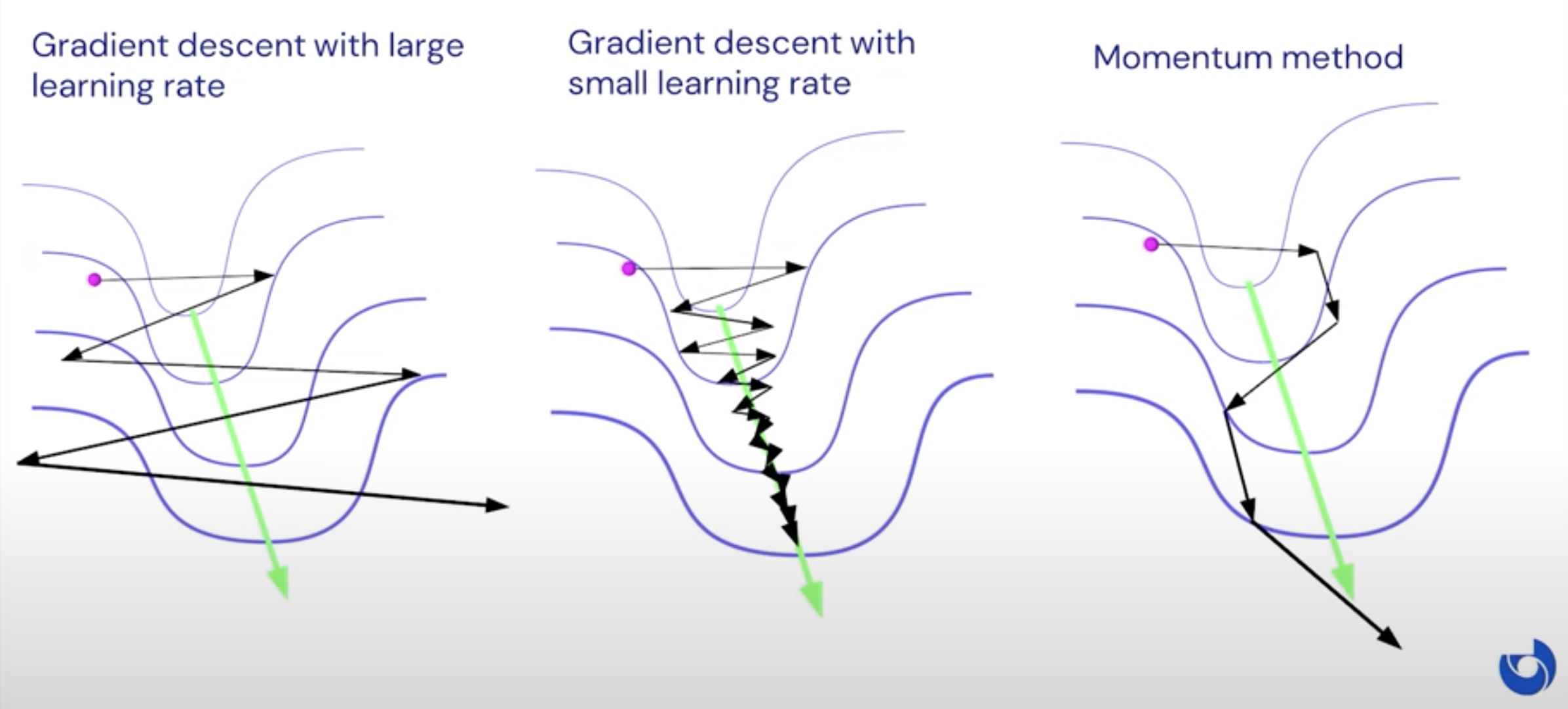image (screenshot from video lecture)

Upper bounds for Nesterov’s momentum variant

Given objective $h(\theta)$ satisfying same technnical conditions, and careful choices of $\alpha_k$ and $\eta_k$,

Nesterov’s momentum method satisfies:

\(h(\theta_k) - h(\theta^*) \leq L(\frac{\sqrt{\kappa}-1}{\sqrt{\kappa}})^k \lVert \theta_0-\theta^* \rVert ^2\)

Convergence theory: 1st-order methods and lower bounds

  • A first-order method is one where updates are linear combinations of observed gradients.

  • included:
    • gradient descent
    • momentum methods
    • conjugate gradients
  • not included:
    • preconditioned gradient descent/2nd-order methods

Lower bounds

No major algorithmic improvement

Comparison of iteration counts

To achieve $h(\theta_k)-h(\theta*) \geq \epsilon$, the number of iterations k satisfies:

  • (Worst case) lower bound for 1st-order methods \(\kappa \in \omega\)
  • Upper bound for gradient descent
  • Upper bound for GD w/ Nesterov’s momentum

4.2nd-order methods

The problem with 1st-order methods

  • Dependency on global condition number:For many 1st-order method, the number of steps needed to converge grows with “condition number”:
\[\kappa = \frac{Max curvature}{Min curvature}=\frac{L}{\mu}\]
  • Depend on the problem:This will be very large for some problems (e.g. certain deep architecture)
  • 2nd-order methods can improve (or even eliminate) this dependency on kappa

Derivation of Newton’s method

  • Approximate h(\theta) by its 2nd-order Taylor series around current \theta:
\[h(\theta + d) h(\theta) + \nabla h(\theta) d +\]

  • Minimize this local approximation to obtain \(d = -H(\theta) \nabla h(\theta)\)

  • Update current iterate with this \(\theta_{k+1} = \theta_{k} - H(\theta)^{-1}\nabla h(\theta_{k})\)

In practice people still use momentum for 2nd-order

Comparison to gradient descent

  • Max allowable global learning rate for GD to avoid divergence:

  • Gradient descent implicitly minimizes a bad approximation of 2nd-order Taylor series:

\[h(\theta+d) \approx h(\theta) + \nabla h(\theta)^\top d + \frac{1}{2} d^\top H(\theta)d\]

Breakdown of local quadratic approximation

  • Quadratic approximation of objective is only trustworthy in a local region around current $\theta$
  • Gradient descent implictly approximates the curvature everywhere by its global max, and so doesn’t have this problem
  • Newton’s method uses $H(\theta)$, which may become an underestimate in the region we are taking out update step

Solution: Constrain update d to lie in a trust region R around, where approximation remains good enough. Subsitute Hessian with LI The curvature is maximum every where

  • LI is too pessimistic/conservative an approximation of the Hessian! It treats all directions as having max curvature.

Trust regions and damping

added to the hessian

  • \(\lambda\) depends on r in a complicated way, but we can just work with directly
  • Some methods allow you to adjust on the fly

Alternative curvature matrices

Hessian may not be the best matrix

H(\theta) does not necessarily give the best quadratic approximation for optimization. Different replacements for could produce a more global approximation or a more conservative approximation.

  • The most important family of related examples includes:
    • Generalized Gauss-Newton Matrix
    • Fisher Information Matrix
    • Empirical Fisher
  • Nice properties versus normal Hessian:
    • always positive semi-definite, that is, no negative curvature
    • give parameterization invariant updates in small learning rate limit unlike Newton’s method.
      • Newton’s method invariant to linear reparametrization of the problem
    • work much better in practice for neural net optimization

Barrier to application of 2nd-order methods for NN

  • For neural networks, $\theta$ can have 10s of millions of dimensions

  • We simply cannot compute and store an n*n matrix, let alone invert it.

  • To use 2nd-order methods, we must simplify the curvature matrix’s

    • computation
    • storage
    • and inversion

This is typically done by approximating the matrix with a simpler form.

Diagonal approximations

Very primitive approximation The simplest approximation: include only the diagonal entries of curvature matrix by setting the rest to 0

Properties:

  • Inversion and storage cost O(n)
  • Computational costs depends on form of original matrix that ranges from easy to hard
  • Unlikely to be accurate, but can compensate for basic scaling differences between parameters

Used in RMS-prop and Adam methods to approximate Empirical Fisher matrix

Block-diagonal approximation

Assuming b b bock size Properties:

  • Storage cost \(\mathcal{O}(bn)\)
  • Inversion cost \(\mathcal{O}(b^2n)\)
  • Similar difficulty to computing diagonal
  • Can only be realistically applied for small block sizes

Well-known example developed for neural nets: TONGA

Kronecker-product approximations

  • Block-diagonal approximations of GGN/Fisher where blocks correspond to network layers
  • Approximate each block as Kronecker product of two small matrices
  • Storage and computation cost \(\mathcal{O}(n)\)
  • Cost to apply inverse \(\mathcal{O}(b^0.5n)\)
  • Used in current most powerful but heavyweight neural net optimizer K-FAC

5.Stochastic optimization

Motivation

  • Typical objectives in machine learning are an average of case-specific losses over training cases: \(h(\theta) = \frac{1}{m} \sum_{i=1}^m h_i(\theta)\)

  • m can be very big, and so computing the gradient gets expensive: \(\nabla h(\theta) = \frac{1}{m} \sum_{i=1}^m \nabla h_i(\theta)\)

Mini-batching

  • There is often significant statistical overlap between \(h_i(\theta)\)

  • Early in learning, when “coarse” features are still being learned, most \(\nabla h_i(\theta)\) will look similar

  • Idea: randomly subsample a mini-batch of training cases of size b, and estimate gradient as \(\nabla h(\theta) = \frac{1}{b} \sum \nabla h_i(\theta)\)

SGD

  • Stochastic GD replaces \(\nabla h(\theta)\) with its mini-batch estimate

  • To ensure convergence,

    • Decay learning rate: \(\alpha_k = \frac{1}{k}\)
    • Use Polyak averaging
    • Slowly increase the mini-batch size during optimization

Convergence of SGD

  • Stochastic methods converge slower than correpsonding non-stochastic ones

asymptotics are not the whole story

  • Iterations to converge No log

Stochastic 2nd-order

  • Mini-batch gradients estimates can be used with 2nd-order and momentums methods too
  • Curvature matrices estimated stochastically using decayed averaging over multiple steps
  • No stochastic optimzation method that sees the same amount of data can have better asymptotic convergence speed than SGD with Polyak averaging
  • Pre-asymptotic performance usually matters more in practice. So stochastic 2nd-order and momentum methods can be useful if
    • the loss surface curvature/condition nnumber is bad enough
    • the mini-batch size is large enough

Conclusions

  • Optimization methods
    • enable learning in models by adapting parameters to minimize some objective
    • main engine behind neural networks
  • 1st-order methods
    • take steps in direction of steepest descent
    • run into issues when curvature varies strongly in different directions
  • Momentum methods
    • use principle of momentum to accelrate along directions of lower curvature
    • obtain optimal convergence rates for 1st-order methods
  • 2nd-order methods
    • improve convergence in problems with bad curvature, even more so than momentum methods
    • require use of trust-regions/damping to work well
    • also require the use of curvature matrix approximations to be practical in high dimensions
  • Stochastic methods
    • use mini-batches of data to estimate gradients
    • asymptotic convergence is slower
    • pre-asymptotic convergence can be sped up with 2nd-order methods and/or momentum

References: Introductory Lectures on Convex Optimization

Numerical Optimization