AI Sequences and Recurrent Networks
The course slides:
1.Motivation
What are sequences?
Element can be repeated Order matters Of variable length
How can we develop models that deal with sequential data?
Summary:
Sequences are collections of variable length where order matters. Sequences are widespread across machine learning applications Not all deep learning models can handle sequential data
2.Fundamentals

Scalability Issues
The model where you condition on the context does capture some of the structure, it is not scalable.
Fixing a small context: N grams
What are N-grams?
Only condition on N previous words!
From Kavita’s beautiful post:
N-grams of texts are extensively used in text mining and natural language processing tasks. They are basically a set of co-occurring words within a given window and when computing the n-grams you typically move one word forward (although you can move X words forward in more advanced scenarios).
For example, for the sentence “The cow jumps over the moon”. If N=2 (known as bigrams), then the ngrams would be:
- the cow
- cow jumps
- jumps over
- over the
- the moon
So you have 5 n-grams in this case. Notice that we moved from the->cow to cow->jumps to jumps->over, etc, essentially moving one word forward to generate the next bigram.
If N=3, the n-grams would be:
- the cow jumps
- cow jumps over
- jumps over the
- over the moon
So you have 4 n-grams in this case. When N=1, this is referred to as unigrams and this is essentially the individual words in a sentence. When N=2, this is called bigrams and when N=3 this is called trigrams. When N>3 this is usually referred to as four grams or five grams and so on.
Downsides of using N-grams
Although it alleviates scalability
- Doesn’t take into account words that are more than N words away
- Data table is still very large
Summary
Modeling probabilities of sequences scales BADLY given the non-independent structure of their elements
Can this probability estimation be learned in a more efficient way?
Learning to model word probabilities
1.Vectorizing the context
\(f_\theta\) summarizes the context in h such that: \(p(x_t | x_1, ..., x_{t-1} \approx p(x_t|h))\)
Desirable properties for \(f_\theta\):
- Order matters
- Variable length
- Learnable (differentiable)
- Individual changes can have large effects (non-linear/deep)
- preserve long-term dependencies
\(f_\theta\) concatenates the N last words.
Summary:
N-grams and simple aggregation do not meet the requirements for modeling sequences.

2.Modeling conditional probabilities
Desirable properties for g:
- Individual changes can have large effects(non-linear/deep)
- Returns a probability distribution
Summary N-grams and simple aggregation do not meet the requirements for modeling sequences.
How can we build a deep network that meets our requirements?
Recurrent Neural Networks
Step 1: Persistent state variable h stores information from the context observed so far.
Step 2: RNNs predict the range y (the next word) from the state h:
Softmax ensures that we obtain a probability distribution over all possible words
Step 3: Input next word in sentence x.
Weights are shared over time steps RNNs rolled out over time
Loss: Cross Entropy
Next word prediction is essentially a classification task where the number of classes is the size of the vocab.
\theta output input update hidden state | For one word | For the sentence | |——-|——–| | \(\mathcal{L}_\theta = -y_t log y_t\) | \(\mathcal{L}_\theta = -y_t log y_t\) |
Differentiating w.r.t.
Recursive loop in the model
three parameter that we need to optimize
backpropagation through time
 h has come from another equaiton
h has come from another equaiton
Vanishing gradients
A big problem in RNN If Wh > 1 , explode
If Wh < 1, vanishing
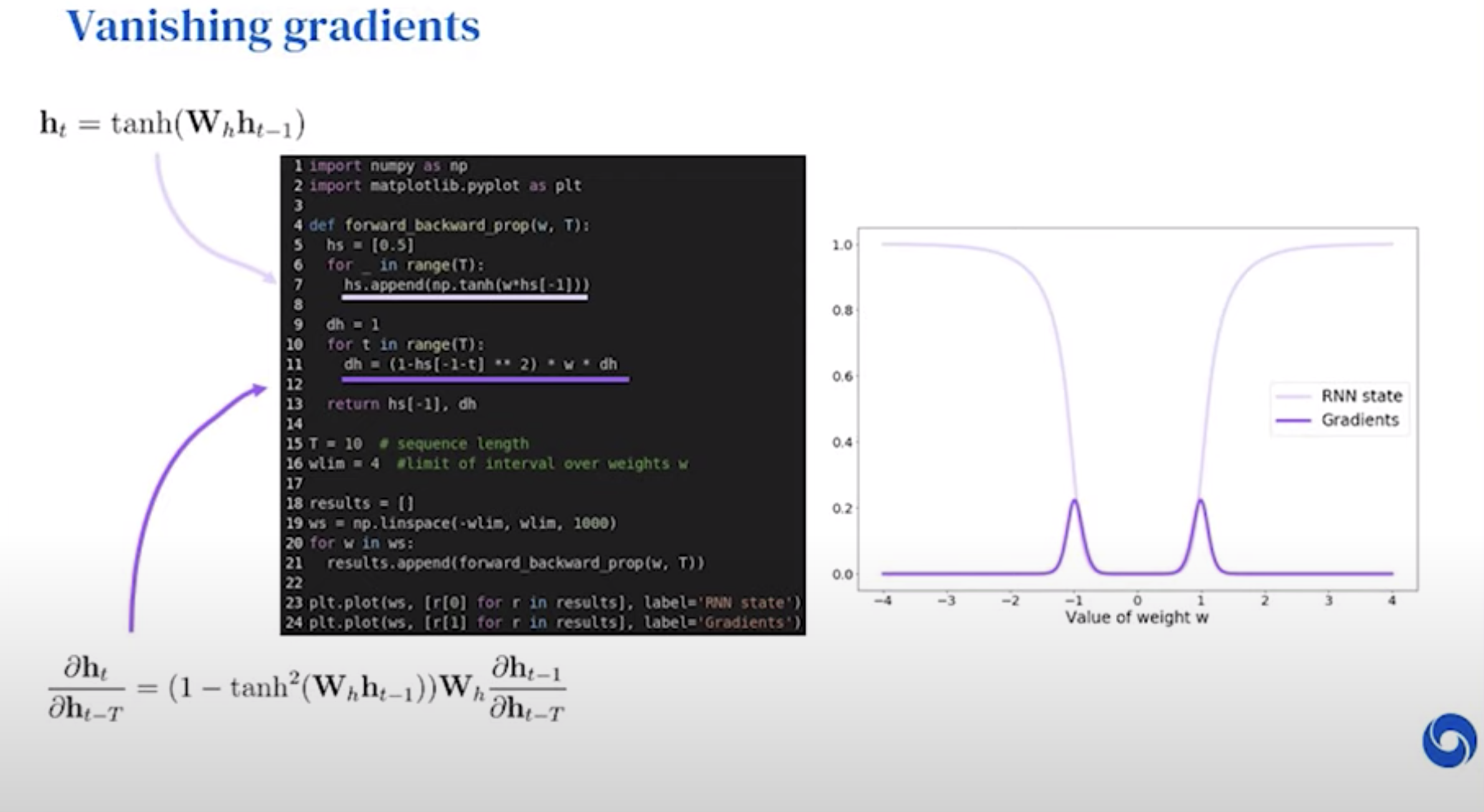 We depend on the gradients in order to update our models. If they are 0, our models won’t learn anything.
We depend on the gradients in order to update our models. If they are 0, our models won’t learn anything.
Must update a couple of times before goes to zero
Summary: RNNs can model sequences of variable length and can be trained via back-propagation.
They do suffer from the vanishing gradients problem, which stops them from capturing long-term dependencies.
Long term dependencies are very important, but RNNs are not equipped to capture those.
How can we capture long-term dependencies?
Long Short-Term Memory networks
Forget gate
Input gate
Output gate
Gated Recurrent Unit nets
GRU can be seen as a simplified LSTM.
It trains faster but LSTM can be stronger.
Summary: LSTMs and GRUs overcome the vanishing gradient problem by making use of sophisticated gating mechanisms.
As a result these models are ubiquitous across machine learning research.
3.Generation
Using a trained model
During training we focused on optimizing the log probability estimates produced by our model.
This means that at test time we can use it to evaluate the probability of a new sentence. This, however, is arguably not very interesting.
An alternative use case of our trained model is sequence generation.
Generating sequences using RNNs
y is a probability distribution over possible words that we can sample from
The sampled y is the input to the next iteration of the network.
Images as sequences
Images as sequences: PixelRNN
Softmax Sampling
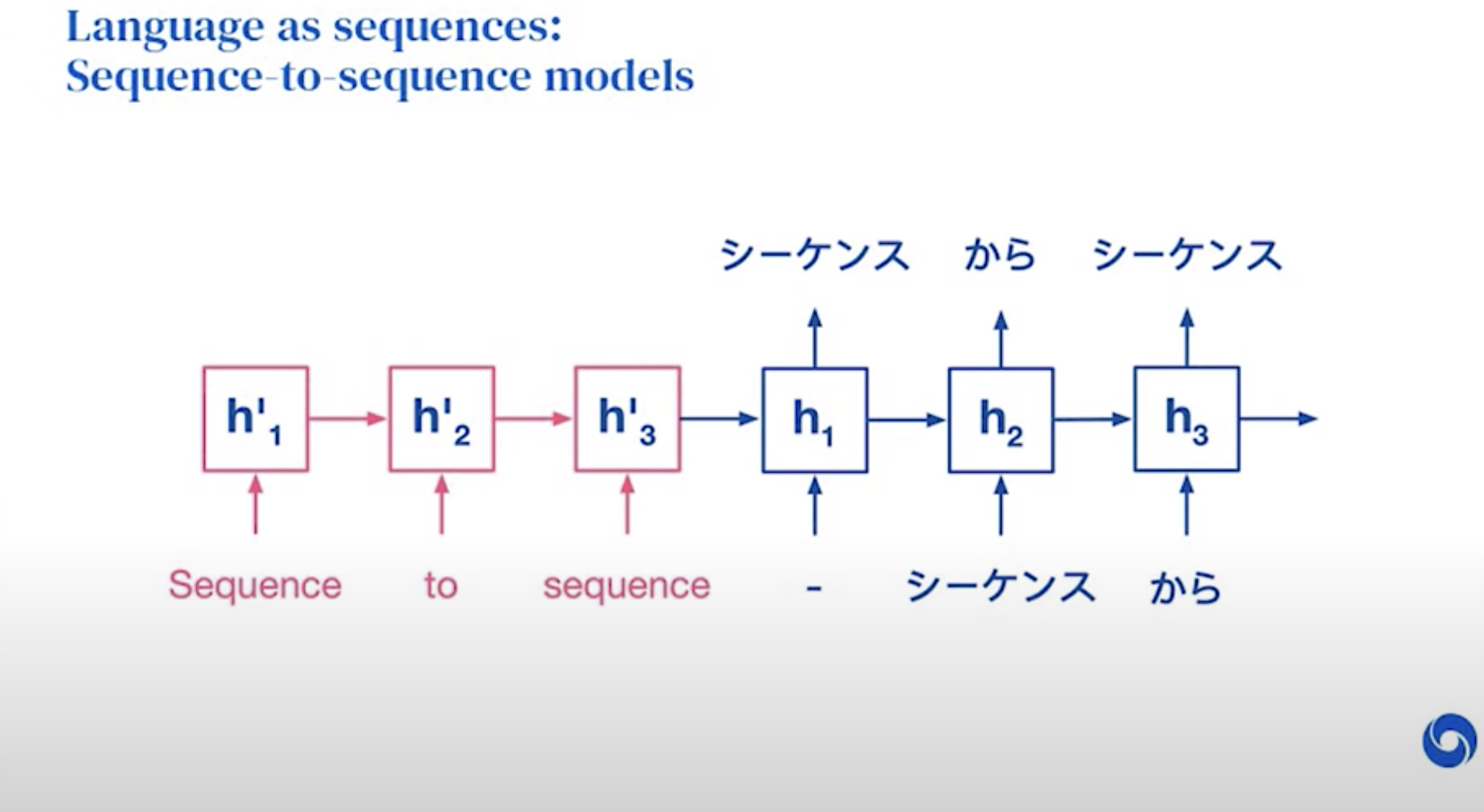
Natural language as sequences
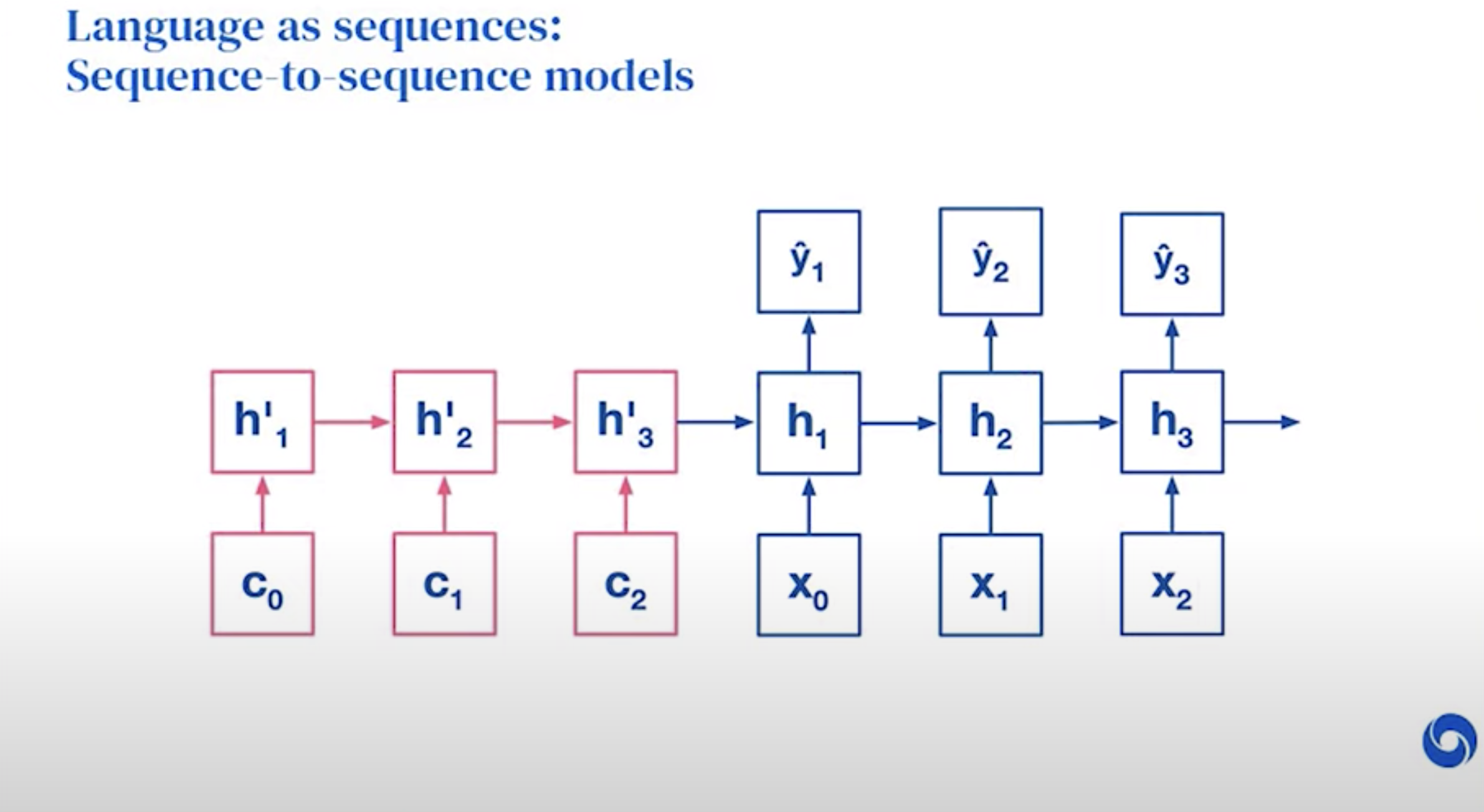
Useful technique for translation!
RNN can be very flexible as to what to condition on :)
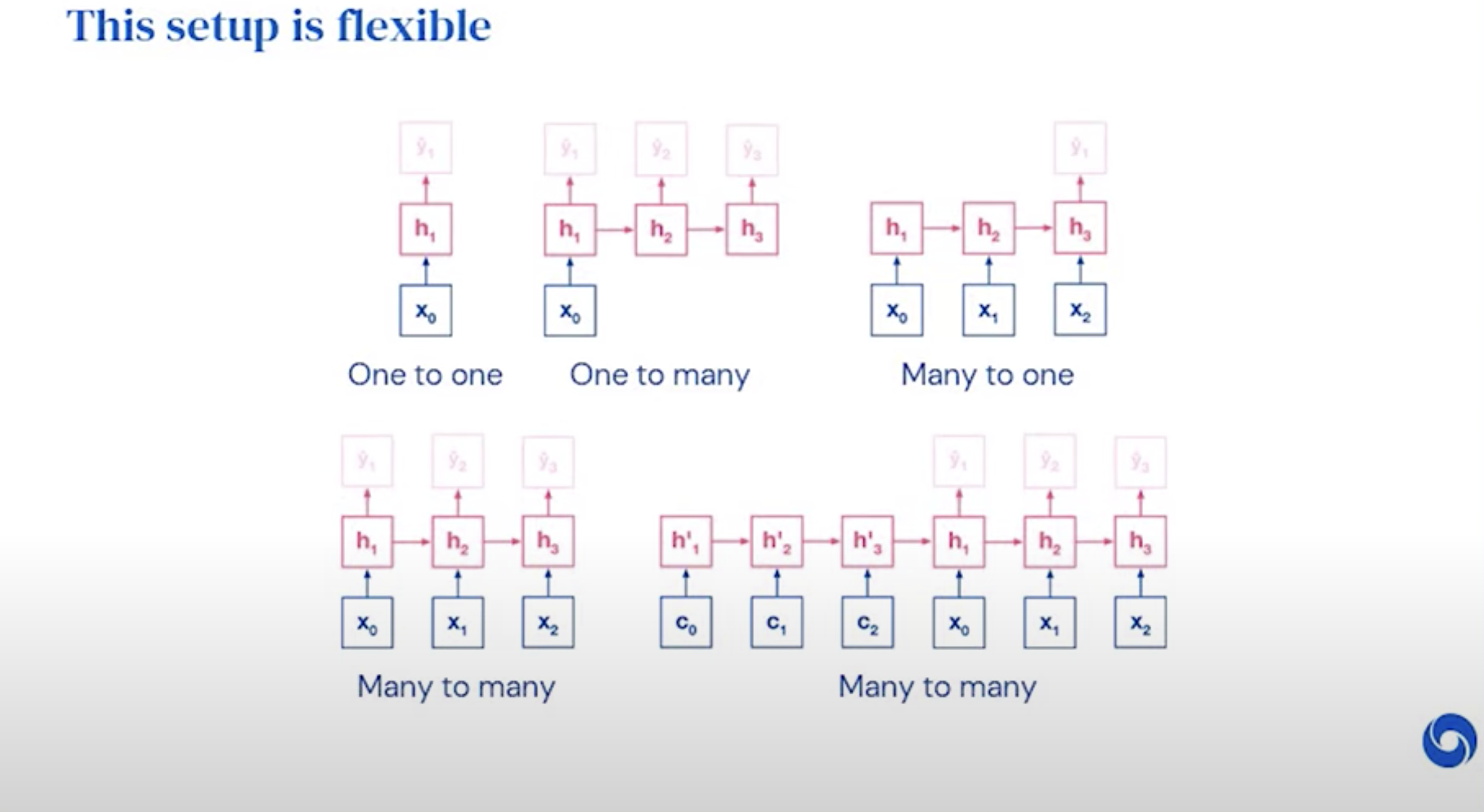
Seq2seq has a wide range of applications
- MT
- Image Captions
- Speech
- Parsing
- Dialogue
- Video Generation
- Geometry
Audio waves as sequences
Policies as sequences
Transformers for sequenes
GPT2
- Transformer-based language model with 1.5 billion parameters for next-word prediction
- Dataset: 40GB of text data from 8M websites
- Adapts to style and content of arbitrary conditioning input
Evolution of language modeling
In 2011, at least a sentence is produced: Generating Text with Recurrent Neural Networks
In 2019, it has popular reference and match the style of tabloid: Better Language Models and Their Implications
Summary:
-
Motivation: Sequences are everywhere but modeling them is hard!
- Covered different approaches:
- N-Grams
- RNNs
- LSTMs & GRUs
- Dilated convolutional and transformers
- These models are flexible and can be applied to a wide range of tasks across machine learning