Introduction

Use of Model-Free Control

Model-free control can solve problems where

  • MDP model is unknown, but experience can be sampled

  • MDP model is known, but is too big to use, except by samples

On/Off-Policy Learning

  • On-policy Learning

    • learn on the job

    • learn about policy $\pi$ from experience sampled from $\pi$

  • Off-policy learning

    • look over someone’s shoulder

    • learn about policy $\pi$ from experience sampled from $\mu$

On-Policy Monte-Carlo Control

$\epsilon$-Greedy Exploration

  • Simplest idea for ensuring continual exploration

  • All m actions are tried with non-zero probability

  • With probability $1-\epsilon$ choose the greedy action

  • With probability $\epsilon$ choose an action at random

$\epsilon$-Greedy Policy Improvement

For any $\epsilon$-greedy policy $\pi$, the $\epsilon$-greedy policy $\pi'$ with respect to $q_\pi$ is an improvement: $v_\pi'(s) \geq v_\pi(s)$ $$P_{ss'} = P[S_{t+1}=s' | S_t=s]$$

GLIE

Greedy in the Limit with Infinite Exploration: - All state-action pairs are explored infinitely many times, - The policy converges on a greedy policy

GLIE Monte-Carlo Control

GLIE Monte-Carlo control converges to the optimal action-value function, Q(s,a) converges to $q_*(s,a)$

  • Sample kth episode using $\pi$

  • For each state $S_t$ and action $A_t$ in the episode

\[N(S_t, A_t) \leftarrow N(S_t,A_t)+1 Q(S_t, A_t) \leftarrow Q(S_t, A_t) + \frac{G_t-Q(S_t,A_t)}{N(S_t, A_t)}\]
  • Improve policy based on new action-value function $$ \epsilon = \frac{1}{k}

\pi = $\epsilon$-greedy(Q) $$

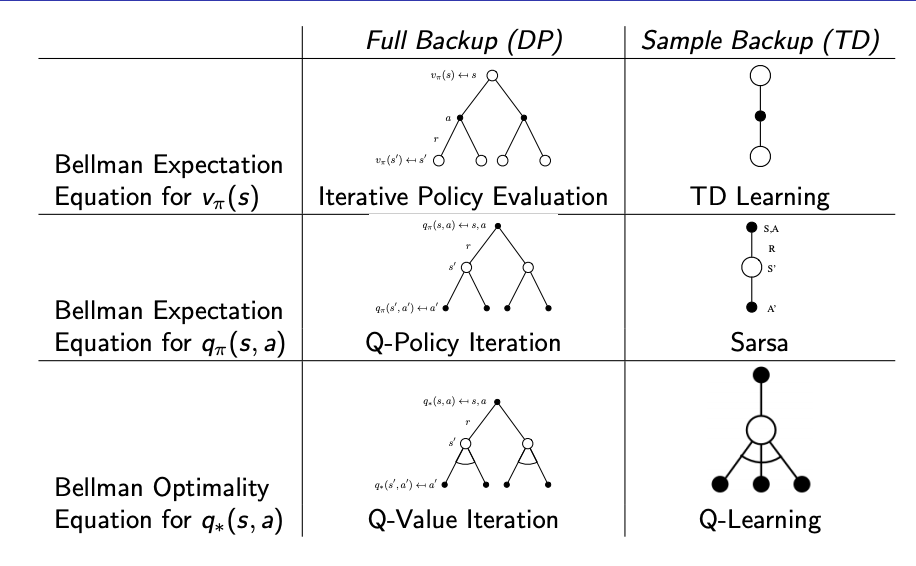
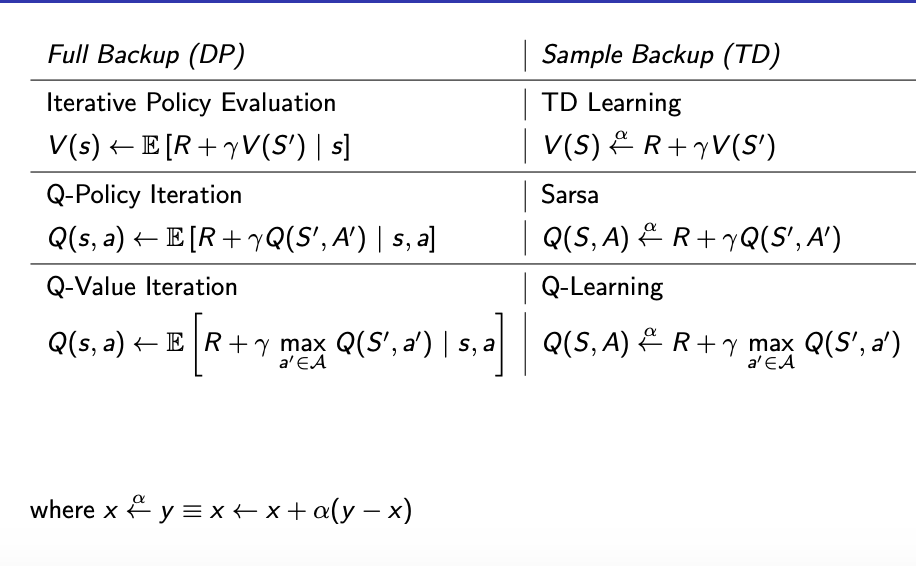
On-Policy Temporal-Difference Learning

Sarsa Algorithm for On-policy Control

Convergence of Sarsa

Sarsa converges to the optimal action-value function, Q(s,a) \rightarrow q_*(s,a), under the following conditions: - GLIE sequences of policies $\pi_t(a | s) - Robbins-Monro sequence of step-sizes $\alpha_t$ $$ \sum_{t=1}^{\inf} \alpha_t = \inf \sum_{t=1}^{\inf} \alpha_t^2 < \inf $$

Forward View Sarsa($\lambda$)

Backward View Sarsa($\lambda$)

  • Like TD($\lambda$), we use eligibility traces in an online algorithm

  • Unlike TD($\lambda$), Sarsa($\lambda$) has one eligibility trace for each state-action pair

  • Q(s,a) is updated for every state a and action a, in proportion to TD-error and the eligibility trace

Off-Policy Learning

  • Evalute target policy \pi(s,a) to compute $v_\pi(s)$ or $q_\pi(s,a)$ while following behavior policy $\mu(a s)$

Why Important?

  • Learn from observing humans or other agents

  • Re-use experience generated from old policies

  • Learn about optimal policy while following exploratory policy

  • Learn about multiple policies while following one policy

Importance Sampling

Importance Sampling for Off-policy Monte-Carlo

  • Use returns generated from $\mu$ to evaluate $\pi$

  • Weight return $G_t$ according to similarity between policies

  • Update value towards corrected return

  • Cannot use if

    • $\mu$ is zero when $\pi$ is non-zero

  • Importance sampling can dramatically increase variance

Importance Sampling for Off-Policy TD

  • Use TD targets generated from $\mu$ to evaluate $\pi$

  • Much lower variance than Monte-Carlo importance sampling

  • Policies only need to be similar over a single step

Q-Learning

  • We now consider off-policy learning of action values Q(s,a)

  • No importance sampling is required

  • Next action is chosen using behavior policy

Off-policy Control with Q-Learning

  • Allow both behavior and target policies to improve

  • Target policy $\pi$ is greedy w.r.t. Q(s,a)

  • Behavior policy $\mu$ is $\epsilon$-greedy w.r.t. Q(s,a)

Q-Learning Control Algorithm

Q-Learning control converges to the optimal action-value function, Q(s,a) -> q_*(s,a)

Q-Learning Algorithm for Off-policy Control

Summary

Relationship between DP & TD

backpropagation

backpropagation